11.7.3多變異分析ANOVAN
在變異分析的過程中,有些資料並非刻意形成,而是因調查或分析產生的特定資訊,無法事先規劃作出等量分組或先經實驗分組。例如,有一些汽車銷售資訊,在銷售單中可能有不同車種、型號、排氣量,甚至出產國別等。若就其分類有些數量並不一定對等,或處於非平衡狀態。多變異分析可以同時處理平衡或非平衡資料,其功能與anova1、anova2略有不同。此模式之架構如下:

其中有相乘之兩項或三項者,即為其間之交互作用(interaction)產生之效應。在所需之X資料向量中,應有其對應之類別資訊。依其類別資訊可以區分為若干層次,此時可將要設為層次之行歸納在一個細胞陣列 group中。其內可有N層之名單,以此指認X資料之歸屬。在group細胞中之名單可以是一向量、文字陣列或文字細胞陣列,以大括符集合起來,惟其個數需與X中之項目相符。其相關語法如下:
p = anovan(x,group)
p = anovan(x,group,'Param1',val1,'Param2',val2,...)
[p,table] = anovan(...)
[p,table,stats] = anovan(...)
[p,table,stats,terms] = anovan(...)
其參數定義大體上與anova1、anova2等指令相同,每個 GROUP中之變數則必須具有與X等量之元素。在分析後之變異數分析表中,將列出GROUP中之變數名稱。另外增加之參數'Paramx',valx,則可說明如下:
| 'Paramx' | valx |
|---|
| 'sstype' | 1, 2, 或 3(預設值)平方和之型式 |
| 'varnames' | 組別名稱預設為 'X1', 'X2', 'X3', ..., 'XN' ,但可利用此參數定義新名稱 |
| 'display' | 顯示ANOVA表,'on' | 'off' |
| 'random' | 以一向量指定群組參數是否為隨機。 |
| 'alpha' | 信任水準(預設值為0.05或95%) |
| 'model' | 決定採用何種函數,如 'linear'其p值僅計算N主效應(預設值); 'interaction'除主效應外尚計算兩者間之交互效應; 'full'計算所有主效應及交互效應。若為整數k(k<=N),則表示計算至k層級。如k=3,表示主效應+兩者間及三者間之交互效應。 若為零壹值矩陣之定義,如[1 0 0] A主效應、[0 1 0] B主效應、[0 0 1 ] C主效應、[1 1 0] AB交互效應、[1 0 1] AC交互效應、[0 1 1] BC交互效應、[1 1 1] ABC交互效應等。 |
在輸出項當中,TERMS矩陣可作為下一次執行ANOVA時,其 MODEL輸入之引數。若MODEL參數不採用隨機型態,其變異分析表T 中之欄位將為TERMS 、SS、DF、奇偶數、均方、F檢測及P值等。若具隨機功能時,則會顯示TERMS之型態(即固定或隨機)、期望均方、F值之除數均方、F值之除數自由度、除數定義、變異項估計值、低限值及高限值等。
輸出參數STATS 的結構包括使用MULTCOMPARE函數之參數及如下項:
coeffs 估計係數
coeffnames 各係數之名稱
vars 組別參數值矩陣
resid 適配模式下之餘數。
具隨機效應時,則另有下列欄位:
ems 期望均方值。
denom 分母定義。
rtnames 隨機項名稱。
varest 變異項估計值(每一隨機項一個)。
varci 各變異項之信任區間
實際上anova2與anovan也可以通用,只是其安排的語法略有不同而已。anova2是將重複的觀察值置於列向,用reps來計算其每組之重複次數,而anovan則必須另外建相關的行作為指示其階數之用。例如下面的例子,假設屬anova2之資料,且是二重複,即reps=2:
X = [25 17 21; 28 18 65; 45 5 60; 42 10 95]
X =
25 17 21
28 18 65
45 5 60
42 10 95
p=anova2(X,2)
p =
0.0175 0.1930 0.2321

上述資料格式若要改為適用anovan,則必須建立對應之行向量。首先建立一個對應三欄的位置m1;其次再建立對應重複的群組m2:
m1=repmat(1:3,4,1)
m2=[ones(2,3);2*ones(2,3)]
m1 =
1 2 3
1 2 3
1 2 3
1 2 3
m2 =
1 1 1
1 1 1
2 2 2
2 2 2
其次,再將X,m1,m2以行向對應起來,如:
X=X(:);m1=m1(:);m2=m2(:);
[X m1 m2]
ans =
25 1 1
28 1 1
45 1 2
42 1 2
17 2 1
18 2 1
5 2 2
10 2 2
21 3 1
65 3 1
60 3 2
95 3 2
此時就可以利用anovan執行分析了。
anovan(X, {m1 m2},2)
ans =
0.0175
0.1930
0.2321
其結果與上述anova1相同。看起來使用naovan好像比較複雜,那是因為轉換為anova1之型式複雜的綠故,若準備資料時就朝naovan之需要處理,則會簡單許多。指令中之參數2即為'model'=2的意思,表示分析結果包括交互作用之影響。若不考慮交互作用,則可以免去,其結果將完全與anova1相同。
下面是一個具三方變異分析之例子,設y為觀察之資料,其餘三組g1、g2、g3為對應之組合項,各組內僅有兩種內容,g1為[1 2]、g2['hi' 'lo']、g3['june' 'may']。由三組內容可知,其項目可為數值,可為文字,但文字必須使用文字字串。
y = [52.7 57.5 45.9 44.5 53.0 57.0 45.9 44.0]';
g1 = [1 2 1 2 1 2 1 2];
g2 = {'hi';'hi';'lo';'lo';'hi';'hi';'lo';'lo'};
g3 = {'may'; 'may'; 'may'; 'may'; 'june'; 'june'; 'june'; 'june'};
利用上述資料進行三方變異分析如下:
>>p = anovan(y, {g1 g2 g3})
p =
0.4174
0.0028
0.9140

輸出項P值包括三個主項所產生之效應,由其變異分析表可知分為x1、x2、x3對應g1、g2、g3等三組。由於沒有第三項參數,故僅列示主效率部份。若需其交互效應則必須加入2之參數在最後一項,或令'model' = 2。三個P值則對應個別零假設(Null Hypothesis)Ho1、Ho2、Ho3之機率值。基本上P值趨近零,對於零假設的成分愈小。例如,Ho2之對應P值0.0028已足夠小到可以認定該組合項下之某一樣本平均值無法與另一組有顯著之差別。在進行此項研斷之前,通常必須先選定P值之顯著水準門檻值,常用的的有0.005或 0.001,依問題的特性而定。
上述的結果並未考慮交互效應,若要增加此項功能,必須在參數方面設定,即令'mode'=2,或直接使用2即可。例如:
>>[p,table]=anovan(y, {g1 g2 g3},'model',2)
p =
0.0347
0.0048
0.2578
0.0158
0.1444
0.5000
table =
'Source' 'Sum Sq.' 'd.f.' 'Singular?' 'Mean Sq.' 'F' 'Prob>F'
'X1' [ 3.7812] [ 1] [ 0] [ 3.7812] 336.1111] [0.0347]
'X2' [199.0013] [ 1] [ 0] [199.0013] [1.7689e+004] [0.0048]
'X3' [ 0.0612] [ 1] [ 0] [ 0.0612] [ 5.4444] [0.2578]
'X1*X2' [ 18.3012] [ 1] [ 0] [ 18.3012] [1.6268e+003] [0.0158]
'X1*X3' [ 0.2112] [ 1] [ 0] [ 0.2112] [ 18.7778] [0.1444]
'X2*X3' [ 0.0113] [ 1] [ 0] [ 0.0113] [ 1] [0.5000]
'Error' [ 0.0113] [ 1] [ 0] [ 0.0113] [] []
'Total' [221.3788] [ 7] [ 0] [] [] []

結果會有三項值,其內容大致相同。P值之首三項為主效應,其餘三項為交互效應。在名稱上均預設為x1、x2、x3,此名稱亦可自行設定:
>>p= anovan(y,{g1 g2 g3},'varnames',{'time' 'limit' 'month'},'model',2);

>> aoctool
Note: 6 observations with missing values have been removed.
AOCTOOL 適合單向變異分析(ANOCVA)及繪製變量圖。其執行格式如下:
AOCTOOL(X,Y,G,ALPHA)
上式之輸入參數:X,Y為對應之資料,其中X為已知值,Y為回應值。G則是作為分組之變數。而ALPHA則是信任水準,其預設值為0.05,亦即其信任水準為95%。
執行這個程式後,將出現三個圖表,其中一個為交談曲線圖,可以調整參數使其產生預測值變化,其二為為變異分析表(ANOVA),另一為參數值預測。
除上述輸入參數外, 各參數尚可指定名稱,其圖表亦可開關。其指令型式如下:
AOCTOOL(X,Y,G,ALPHA,XNAME,YNAME,GNAME,DISPLAYOPT,MODEL)
其中XNAME,YNAME,GNAME分別為X軸、Y軸及組別名稱。 DISPLAYOPT 則控制圖形是否顯示('on'為預設值,或否'off'), MODEL 則控制最初適配時之選項,包括:
1 'same mean' (共同均值)
2 'separate means' (分開均值)
3 'same line' (共同預測線)
4 'parallel lines' (平行預測線)
5 'separate lines' (分離預測線)
此外,此一指令亦容許有輸出,其型式如下:
[H,ATAB,CTAB,STATS] = AOCTOOL(...)
其中 H代表圖中各線之握把, ATAB 與 CTAB則為ANOVA表及係數表之內容,而 STATS則為多重均值比較之結果,亦即為 MULTCOMPARE 函數執行的結果。
下面的例子中為利用load carsmall下載最近十餘年(1970-1982)的汽車相關資料。其中包括車重(Weight)、加侖里程數(MPG)及年份(Model_Year)。其資料內容如下,請特別注意在加侖里程之資料中有六點之資料從缺。
>> Weight'
3504 3693 3436 3433 3449 4341 4354
4312 4425 3850 3090 4142 4034 4166
3850 3563 3609 3353 3761 3086 2372
2833 2774 2587 2130 1835 2672 2430
2375 2234 2648 4615 4376 4382 4732
2464 2220 2572 2255 2202 4215 4190
3962 4215 3233 3353 3012 3085 2035
2164 1937 1795 3651 3574 3645 3193
1825 1990 2155 2565 3150 3940 3270
2930 3820 4380 4055 3870 3755 2605
2640 2395 2575 2525 2735 2865 3035
1980 2025 1970 2125 2125 2160 2205
2245 1965 1965 1995 2945 3015 2585
2835 2665 2370 2950 2790 2130 2295
2625 2720
>> MPG'
18.0000 15.0000 18.0000 16.0000 17.0000 15.0000 14.0000 14.0000
14.0000 15.0000 NaN NaN NaN NaN NaN 15.0000
14.0000 NaN 15.0000 14.0000 24.0000 22.0000 18.0000 21.0000
27.0000 26.0000 25.0000 24.0000 25.0000 26.0000 21.0000 10.0000
10.0000 11.0000 9.0000 28.0000 25.0000 25.0000 26.0000 27.0000
17.5000 16.0000 15.5000 14.5000 22.0000 22.0000 24.0000 22.5000
29.0000 24.5000 29.0000 33.0000 20.0000 18.0000 18.5000 17.5000
29.5000 32.0000 28.0000 26.5000 20.0000 13.0000 19.0000 19.0000
16.5000 16.5000 13.0000 13.0000 13.0000 28.0000 27.0000 34.0000
31.0000 29.0000 27.0000 24.0000 23.0000 36.0000 37.0000 31.0000
38.0000 36.0000 36.0000 36.0000 34.0000 38.0000 32.0000 38.0000
25.0000 38.0000 26.0000 22.0000 32.0000 36.0000 27.0000 27.0000
44.0000 32.0000 28.0000 31.0000
>> Model_Year'
70 70 70 70 70 70 70 70 70 70 70 70 70 70
70 70 70 70 70 70 70 70 70 70 70 70 70 70
70 70 70 70 70 70 70 76 76 76 76 76 76 76
76 76 76 76 76 76 76 76 76 76 76 76 76 76
76 76 76 76 76 76 76 76 76 76 76 76 76 82
82 82 82 82 82 82 82 82 82 82 82 82 82 82
82 82 82 82 82 82 82 82 82 82 82 82 82 82
82 82
利用AOCTOOL分析時,設車重為輸入值,加侖里程為對應值,年份作為組別,其指令格式如下:
aoctool(Weight,MPG,Model_Year,0.05)
actool
上圖為依年份所得之預測值,共有三個不同年份,可以依年份之類別選擇顯示。由此圖可知車重增加時,每加侖之里程數將減少。且年份愈近者,其每加侖之里程數愈高。
在模式(Model)中,則可選不同的預測線處理方式。

此表則表示三條預測線之截距與斜率。就截距而言,總截距為45.9798,70年份則比此值略低-8.5805,亦即45.9798¬-8.5805=37.3993。總的斜率為-0.0078,70年份則比此值略高0.002,或為-0.0058。如此類推,即可看出統計上之預測值。其對應之標準差及T試驗值則附於其後。各組之公式如下:
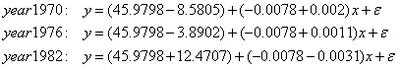

就變異分析表(ANOVA)分析,年份及重量均相當顯著,其交叉效果也在0.0072之水準,亦在顯著之範圍,此可由圖中82年份與其他年份在車重4000公斤有交叉的現象有關。
若使用參數輸出的方式,則可執行如下指令:
[h,a,c,s] = aoctool(Weight,MPG,Model_Year,0.05)
Note: 6 observations with missing values have been removed.
h =
152.0028
153.0013
154.0013
204.0013
205.0013
206.0013
207.0013
208.0013
a =
Columns 1 through 5
'Source' 'd.f.' 'Sum Sq' 'Mean Sq' 'F'
'Model_Year' [ 2] [ 807.6896] [ 403.8448] [ 51.9762]
'Weight' [ 1] [2.0502e+003] [2.0502e+003] [263.8679]
'Model_Year*Weight' [ 2] [ 81.2188] [ 40.6094] [ 5.2266]
'Error' [ 88] [ 683.7420] [ 7.7698] []
Column 6
'Prob>F'
[1.2212e-015]
[ 0]
[ 0.0072]
[]
c =
'Term' 'Estimate' 'Std. Err.' 'T' 'Prob>|T|'
'Intercept' [ 45.9798] [ 1.5208] [ 30.2330] [2.9266e-048]
' 70' [ -8.5805] [ 1.9619] [ -4.3737] [3.3417e-005]
' 76' [ -3.8902] [ 1.8686] [ -2.0818] [ 0.0403]
' 82' [ 12.4707] [ 2.5568] [ 4.8775] [4.7391e-006]
'Slope' [ -0.0078] [5.5717e-004] [-14.0031] [4.0955e-024]
' 70' [ 0.0020] [6.6152e-004] [ 2.9605] [ 0.0039]
' 76' [ 0.0011] [6.5328e-004] [ 1.7425] [ 0.0849]
' 82' [ -0.0031] [9.9914e-004] [ -3.0994] [ 0.0026]
s =
source: 'aoctool'
gnames: {3x1 cell}
n: [3x1 double]
df: 88
s: 2.7874
model: 5
slopes: [3x1 double]
slopecov: [3x3 double]
intercepts: [3x1 double]
intercov: [3x3 double]
pmm: [3x1 double]
pmmcov: [3x3 double]















 預測圖
預測圖
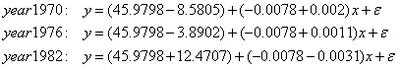






 指令polytool之交談圖
指令polytool之交談圖















