11.8內插法

內插技巧是資料分析時常用的工具，尤其在尋求等距之對應資料作為比對時，常需利用內插法尋求實際對應之值。當然內插法亦可用來尋求資料間之中間對應值。在MATLAB中有下列指令處理內插法：

指令名稱	說明
interp1,interp1q	一維內插法，有如查表法。interp1q與interp1功能相同，但執行速度較快。
interp2	二維內插指令
interp3, interpn	三維及多維內插指令
spline	曲尺內插

以東方人體型之身高與體重標準為例，其對應資料如下：

身高  157.5  160 162.5 165  167.5  170   172.5  175   177.5 180
小體型 52.5  54   55    57   58    59.5  61.5   63.5   66   67.5
中體型 56    57.5 59    60   61.5  63.5  66     67.5   69   71
大體型 60    61.5 63.5  65   67    68.5  70.5   72.5   74   76.5

由上表可直接查得160cm對應之中體型重為57.5kg。但若要知道中間值，例如，161cm身高的人的體重則必須用內插法。所以內插法之使用有一個特徵是其相關值是連續增加或減少或具有相關性的。因此利用內插法較不易失敗。尋求內插值可以使用上述幾個指令，但若屬一維的對應，則仍以使用interp1為多，其呼叫之型式如下：

YI = INTERP1(X,Y,XI)

這個指令類似查表法，前面X,Y其實是一個對應表，後面之XI則是要查之進入值，而所得之結果則置於左邊之YI。此處，X,Y必須是一個對應的向量，XI則可為向量或常數值，其個數亦不必與X,Y相同。只是所得之YI的個數亦會與XI相同。以上述之身高體重為例，若要知道161、163、171cm等高度之對應中體型體重時，則可呼叫如下：

height=[157.5 160 162.5 165 167.5 170 172.5 175 177.5 180];
M_wt=[56 57.5 59 60 61.5 63.5 66 67.5 69 71];
YI=interp1(height,M_wt,[161 163 171])

YI =
58.1000   59.2000   64.5000

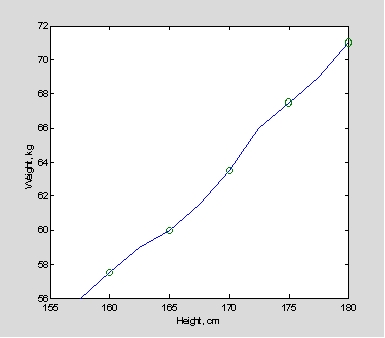
利用上項功能，實際上也可以重新定域新範圍，並獲得新的對應值。例如希望能獲得150,155,160,165,179,175,180之對應體重，並由此作圖，則可以執行如下：

H=[160:5:180];
W=interp1(height,M_wt, H);
plot(height,M_wt,H,W,'o');xlabel('Height, cm');ylabel('Weight, kg')

使用同樣的資料，若想查尋58、62、70kg人的對應身高時，亦可利用interp1指令查詢之，只是其順序必須稍加更動：

XI=interp1(M_wt,height,[58 62 70])
XI =
160.8333  168.1250  178.7500

上述之指令中，實際上它內部採用之內插技巧是內設為線性內插，亦即兩點間均以直線作為考量。為求精確，有些內插必須採用特定的方法。在interp1的指令中，實際上亦提供此項選擇，其參數位置如下：

 YI = INTERP1(X,Y,XI,'method')

不同的技巧則在'method'處表示。可以選擇如下幾種：

   'linear'   - 線性內插（預設值）。
   'spline'   - 區段立方曲線內插。
   'nearest'  - 以最靠近的點進行內插。
   'pchip'    - 保留外形區段立方內插（Hermite型）。
   'cubic'    - 與 'pchip'同。

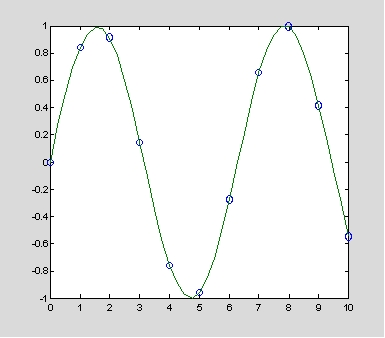
一般之內插法預設為線性，故若需繪圖，並取得較為平滑曲線，則可選用 'spline'，或稱為立方曲線。下面為線性與立方曲線所顯示出不同的效果：

     x = 0:10; y = sin(x); xi = 0:.25:10;
yi = interp1(x,y,xi); plot(x,y,'o',xi,yi)

由於原來之分點之區隔較粗，故僅能顯示直線的曲線。若採用 'spline'的功能，則會產生比較平滑的曲線：

yi = interp1(x,y,xi,'spline'); plot(x,y,'o',xi,yi)

指令中之X參數可以省略，但此時指令用X=[1 2 …length(Y)]為其參數。與rnterp1指令類似的有rnterp1q，後者之功能大體與前者相同，只是後者執行較快，適用於不等距之間隔，因為其輸入值並未經嚴格檢查。但此指令使用時，Ｘ之值必須為單一對應值，且須遞增排列；而Ｙ則需為行向量，若為矩陣則其長度應與X相同。