11.10 spline指令

由於立方曲線之內插可產生較為平滑的曲線，故常為內插法的選項。為此，MATLAB特別另建一指令處理立方曲線之內插。立方曲線內插係以三次方多項式表示，其基本型式如下：

　yi(x)=c1(x-xi)3+c2(x-xi)²+c3(x-xi)+c4

其中i代表每一待內插之區間， ，若總共有n點，則 其中之係數 則必須利用內插之求法求解。其邊界條界如下：

 此多項點必須通過區段之兩端 。
 相鄰兩個多項式在共同端點之斜率（第一導數）必須一致。
 相鄰兩個多項式在共同端點之曲率（第二導數）必須一致。

要求出上項係數 ，可以使用sprine指令之另一種型式：

　　pp=spline(x,y)

這是一個中間結果的型式，因為實際要知道其係數值的不多，大部份都是直接得到內插對應值即可。上述指令之(x,y)為基本資料輸入，pp則為結構變數。其內有form、breaks、coefs等變數。比較重要的是其breaks之Ｘ值基點及對應之係數coefs。依結構變數之呼叫法即為pp.breaks及pp.coefs。以下為執行例：

x=[10  12 14 17];y=[120 140 150 175];
pp=spline(x,y)
pp.breaks
pp.coefs

pp =
    form: 'pp'
  breaks: [10 12 14 17]
   coefs: [3x4 double]
  pieces: 3
   order: 4
     dim: 1
ans =
  10    12    14    17
ans =
  0.2738   -2.8929   14.6905  120.0000
  0.2738   -1.2500    6.4048  140.0000
  0.2738    0.3929    4.6905  150.0000

因此，由上述得到之係數可以代入內插多項式：



上述之資訊對內插之結果並沒什麼幫助，但有時需要這些係數以作為其他指令之用途。但所得之結果亦可利用y=ppval(pp,x)指令得到內插之結果。在spline(x,y)之指令中，若 Y之元素項比Ｘ多二項時，其最初及最後項將用為設定立方曲線之端點斜率之用。若 Y為一向量，亦即：

      f(X) = Y(2:end-1),  Df(min(X))=Y(1),    Df(max(X))=Y(end)

例如：

     x = -4:4; y = [0 .15 1.12 2.36 2.36 1.46 .49 .06 0];
     cs = spline(x,[0 y 0]);
     xx = linspace(-4,4,101);
     plot(x,y,'o',xx,ppval(cs,xx),'-');

基本上，spline指令亦可直接進行內插，輸入項及可以呼叫型式如下：

 YI = SPLINE(X,Y,XI)

例如：

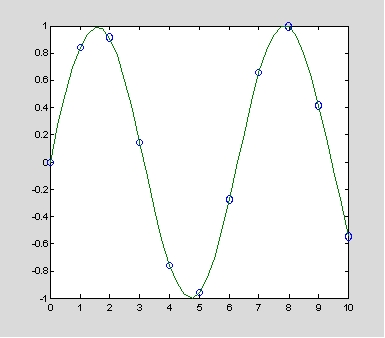
      x = 0:10;  y = sin(x);
      xx = 0:.25:10;
      yy = spline(x,y,xx);
      plot(x,y,'o',xx,yy)

實際上YI = SPLINE(X,Y, XI)等同 YI = PPVAL(SPLINE(X, Y), XI) 。前面所述PP=SPLINE(X,Y)之指令，也可以使用 PP = UNMKPP(BREAKS, COEFS)或 PP = UNMKPP(SPLINE(X,Y))獲得同樣的效果。其中BREAKS為ｘ之向量，而 COEFS則為三次方多項式之係數。