10-2 範例五：簡易之熱流分析

範例五：熱流問題

熱流的問題有時是一個平面分佈的情形。以下圖為例，在一個侷限的空間中，設將其分為四等分，每等分之接觸面積均相同。進口處之溫度為Ｔi，出口溫度為To，其餘外圍部份均為絕熱狀態，熱流停止，故接觸之該面溫度不起變化。同樣，若將熱流比做電流，則可以形成類比電路如圖(b)，設其進出介面時之熱阻以Ｒ表示。由於材質假設相同，其截面積也相同，故每一介面之熱阻也應相同。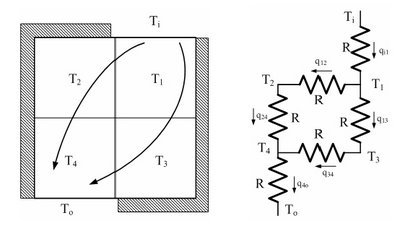


　　　　
由電路之網絡觀之，熱流由外界流入T1節點，再分兩路流入T2與T3兩節點，最後滙流至T4，由此流至外界To。注意T1不能直接流至T4，因為兩者之接觸面積為零。因此由電路網絡很容易解出此並聯電路之解。由於熱阻均相同，在公式中可以不考慮。其熱流之平衡式可表列如下：


　　
根據熱流之關係，可以改變為：




　　　
由上式得到的結論是任何一點之溫度應為其相連週圍之溫度點之平均值。其聯立方程式最後為下列型式：

程式內容

function [T]=heat_plate(ti,to)
% Prog calculating heat transfer through a plate.
% Inputs:
%   ti,to: input & output temperature, C
% Outputs:
%   temp:temperatures at each layer,C
% Example:
%  T=heat_plate(20,-10)
C=[ti 0 0 to]';
A=[3 -1 -1 0;-1 2 0 -1;-1 0 2 -1;-1 -1 0 3];
TT=A\C;T=[ti TT' to];

執行範例

>> T=heat_plate(100,-10)
T =  100.0000   68.5714   52.8571   52.8571   37.1429  -10.0000

深入分析

如果要更確的數據，則可以增加方格，但其運算方程式之數目亦將增加。例如增加為3X3方格，則總格數為九格，必須要有九條方程式才能處理。根據前面所述之原理，某格之溫度等於其鄰近方格溫度之平均值。因此T5之溫度應為T2、T4、T6、T8等四溫度之平均值；而T3與T7則僅為鄰近兩項值之平均，其餘均為三個鄰近值之平均。


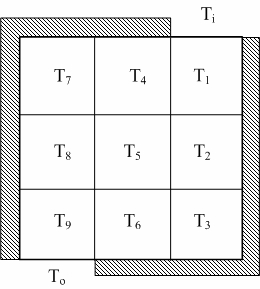
若將其改為矩陣AT=C之型式，則各矩陣之內容變為：

程式內容

　 　　
function [T]=heat_plate3(ti,to)
% Prog calculating heat transfer through a plate by 3x3.
% Inputs:
%   ti,to: input & output temperature, C
% Outputs:
%   temp:temperatures at each layer,C
% Example:
%  T=heat_plate3(20,-10)
C=[ti 0  0  0  0  0  0  0 to]';
A=[3 -1  0 -1  0  0  0  0  0;
　-1  3  0 -1 -1  0  0  0  0;
   0 -1  2  0  0 -1  0  0  0;
  -1  0  0  3 -1  0 -1  0  0;
   0 -1  0 -1  4 -1  0 -1  0;
   0  0 -1  0 -1  3  0  0 -1;
   0  0  0 -1  0  0  2 -1  0;
   0  0  0  0 -1  0 -1  3 -1;
   0  0  0  0  0  -1 0 -1  3];
TT=A\C;T=reshape(TT,3,3);

執行例：

>> T=heat_plate3(20,-10)
T =
12.4272    8.2767    6.0922
 9.0049    6.3107    3.9078
 6.5291    4.0534   -0.6796