12.2 差分函數diff

12.2 差分函數diff

對於一個向量，差分函數在於求取該數列元素間之差異及其導數，相關指令格式如下：

Y = diff(X)
Y = diff(X,n)
Y = diff(X,n,dim)

若Ｘ為向量，則上述指令在於計算其相鄰元素間之差，亦即：

[X(2)-X(1)  X(3)-X(2) ... X(n)-X(n-1)]

若Ｘ為矩陣，則結果將計算其相鄰列間之差，如：

 [X(2:n,:) - X(1:n-1,:)].

參數n為階數，n=1時，其結果與Y = diff(X)相同，n=2時，其結果為diff(diff(X))，依此類推。因此每相差1其項數將減少一項。參數dim則是控制行向或列向差分，dim=1行向（預設值），dim=2為列向。

例：

>> x = 2:2:10
x =
  2     4     6     8    10

>> y=diff(x)
y =

  2     2     2     2

>> y=diff(x,2)
y =

  0     0     0

若間矩較細，將過差分後，其結果應為原函數之導數。

h = .01;
x = 0:h:pi;
d=diff(sin(x.^2))/h;
plot(x,sin(x.^2),x,[0 d],'r:')

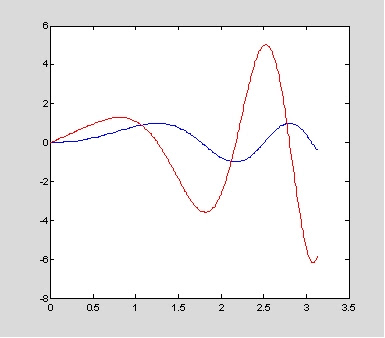
上例等於計算sin(x.^2)之導數 2*cos(x.^2).*x，注意d值之長度會比x少１。

例：

>>X=(1:10).^2,

X =
1     4     9    16    25    36    49    64    81   100　

　>>x1=diff(X),x2=diff(X,2), x3=diff(y)

x1 =
3     5     7     9    11    13    15    17    19
x2 =
2     2     2     2     2     2     2     2
x3 =
2     2     2     2     2     2     2     2

結果為x1比Ｘ少一項，x2比x1又少一項，x2與x3相同，證明y3=diff(diff(X))。
例：

 X = [3 7 5 3;  2 0 8 4]
 x1=diff(X,1), x2= diff(X,1,2)

X =
3     7     5     3
2     0     8     4
x1 =
-1    -7     3     1
x2 =
4    -2    -2
-2     8    -4

例：正弦函數sin(t)以常態分布繪出[0 pi]間之區線及其第二導數cos(t)。

t=[0:pi/50:pi];nn=length(t);td=cos(t);
y=sin(t)+0.05*(randn(1,nn)-0.5);
dt1=diff(y)./diff(t);%backward(+)
dt2=(y(3:nn)-y(1:nn-2))./(t(3:nn)-t(1:nn-2));
plot(t,sin(t));hold on;plot(t,y,'b.');
plot(t,cos(t),'r:');
plot(t(1:nn-1),dt1,'k+');
plot(t(1:nn-2),dt2,'bo');

'+':向後差分；'o'中央差分

由其結果比較，中央差分比向後差分之誤差為小。可由其與實際值之相關係數可以確定。就向後差分者，相關係數為0.4927；而中央差分則為0.7674。

[r1,p1]=corrcoef(t(1:nn-1),dt1)
[r2,p2]=corrcoef(t(1:nn-2),dt2)

r1 =
1.0000   -0.4927
-0.4927    1.0000
p1 =
1.0000    0.0003
0.0003    1.0000
r2 =
1.0000   -0.7674
-0.7674    1.0000
p2 =
1.0000    0.0000
0.0000    1.0000

由於diff之前減特質，所以其功能亦可用來決定某些向量之特性，例如屬增加序列或減少序列，或所謂之單向(monotonic)系列，或屬等距分佈之系列等。下面的例子可作為一般之應用：

• diff(x)==0　測試重複性之元素
• all(diff(x)>0)　測試其單向性
• all(diff(diff(x))==0)　測試各元素是否等距分佈