10.2 線性聯立方程式矩陣解法
所謂線性方程式係指方程式中之變數僅屬一階者,其幕次不能大於一,且任何項中不得有兩變數相乘或相除之情形。在矩陣表示法上,通常採用[A][x]=[b]之型式,其解為[x]=[A]\[b]或[x]=[b]/[A]。
對於線性聯立方程式目前已經發展出許多種解法,其中包括變數迭代消去法及克雷蒙法(Creamer's Method)。目前MATLAB 所使用之解法則以變數迭代消去法為主,或稱為高斯(Gauss Elimination)消去法。這是利用兩線性方程式分別乘以某特定常數,使其與另一方程式之同一變數係數相同,因而兩式相減得以消除該變數。如此展轉消除,最後可以得聯立方程之解。茲舉例說明如下:
3x +4y =10
5x -2y =8
上述聯立方程式中,先將第一式乘兩邊5、第二次兩邊乘3,兩式相減,即可得:
5(4y) - 3(-2y) = 5* 10 - 3*8
由上式整理之後,可得果為y = 1;代入原式任一式可得x = 2,終得解。如果利用第九章之繪圖指令可以繪出此兩條曲線,由其交點即可得到相同的解。
ezplot('3*x+4*y-10',[-10,10]);hold on
ezplot('5*x-2*y-8',[-10,10])
利用這樣的解法並不是解線性方程式之重點,因為線性代數方程式可用矩陣的型式表示,甚至以矩陣之乘除法可以得解。以上面之聯立線性方程式為例,可以化成AX=C之型式,設x=x1,y=x2:

左除法求解
利用MATLAB求解時,只要用矩陣倒除即可,或稱為左除法。例如一組聯立方程式以矩陣表示為[A][X]=[C]時,其未知數項[X]可以利用MATLAB倒除的指令求得,即[X]=[A]\[C]:
A=[3 4;5 -2];
C=[10;8];
X=A\C
X =
2
1
結果立即得到x1=2、x2=1。
反矩陣法求解
解上式矩陣有時可用反矩陣法。反矩陣有倒數的意義,但在矩陣中必須為方矩陣,且須為非特異矩陣(non-singular)。通常用(-1)次方表示之,如A-1 。其基本特質為與原矩陣相乘後,將得到單位矩陣I:
A-1A=AA-1=I
以此乘於AX=C之兩側,可得:
A-1AX=A-1C 或A-1AX=IX=X= A-1C
在MATLAB反矩陣A-1 之求法為inv(A);I或稱為單位矩陣,表示為eye(A)。就上面之聯立方程式之解,可以用MATLAB演算如下:
A=[3 4;5 -2];
C=[10;8];
X=inv(A)*C
X =
2.0000
1.0000
所得的結果與前述之分析相同。理論上雖然如此,在演算時求反矩陣較費時間,使用左除法是
為較佳的操作法。
範例:有一組聯立方程式如下:
6x - 3y +5z = 12
10x + 4y -8z =-20
-6x + 2y +3z = 15
解:先安排A及C矩陣,再利用左除法求得[X]。
A=[6 -3 5;10 4 -8;-6 2 3];C=[12 -20 15]';
x=A\C
C=A*x
x =
0.0479
2.1737
3.6467
C =
12.0000
-20.0000
15.0000
由上述的計算,可以迅速得到結果,即 x= 0.0479, y= 2.1737, z= 3.6467。通常利用MATLAB解聯立方程式,亦會碰到無解的情形,此時或稱為特異狀況(或 |A| 為零的情形)。前述之左除結果,可用以反求C值,C=Ax,其結果也正確。
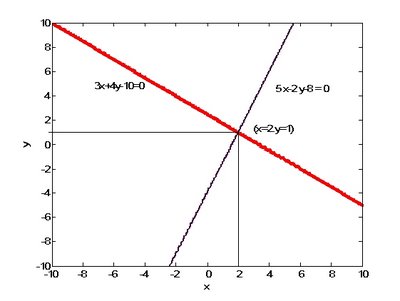 圖10.1
圖10.1
2 則留言:
當C=[0,0,0]的時候怎麼做?
張貼留言