10.5 網絡分析之應用

梯形數值分析法(Trapezoidal Numerical Integration)

數值分析法常用以解積分的問題，積分之解法依問題的性質有不同的方式。比較簡單的方式是將其分成細段，然後細段之微小面積，加總後成為最後的結果。此種積分稱為梯形法。



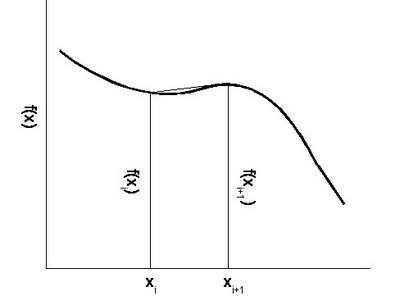
利用梯形法可以解決複雜函數之積分問題。在MATLAB之中，也有相同的指令，TRAPZ，其語法如下：

  Z = trapz(Y)
  Z = trapz(X,Y)
  Z = trapz(...,dim)

若參數中僅有Ｙ項，則其分段值設為1；若區段不為１，則可就其結果乘以需要之區段值。Ｙ值可為複數，可以針對實數及虛數部份分開積分。若有對應之X值，則X與Y應為成對的向量，此時區間可不必均等值。若為長方形矩陣，則可利用第三個參數dim決定是進行行向(=1)或列向(=2)積分。

下面的程式則是就f(x)=1/x函數，在區間A=1與B=2之間作積分，設此區間分成N=10段，進行比較直接運算與使用trapz指令所得的結果：

% trapezoid.m
% Find the area under a curve.
%
f=@(x) 1./x;
A=1;B=2;N=10;
x=linspace(A,B,N);
y=f(x);
Ts=0;
for i=1:N-1,
   DX=x(i+1)-x(i);
   Ts=Ts+DX*(y(i+1)+y(i))/2;
end
Area=trapz(x,f(x));
disp(['¨Using trapezodal law:',num2str(Ts)]);
disp(['¨Using Matlab trapez command:',num2str(Area)]);

執行trapezoid.m程式後，結果如下：

>> trapezoid
¨Using trapezodal law:0.69392
¨Using Matlab trapez command:0.69392

兩者之結果完全吻合。讀者可使用不同之函數及區間，作不同的演算，並相印證。

三角形面積

前面已經討論過如何應用程式指令計算由三個節點構成的三角形面積。但在有限元素法的作業上，通常均採用直接與座標點具有關連的結果，即：



這是一個行列式值，也可以看成矩陣。

其對應的三角形面積Ｓ＝det(A)/2。此時(x1, y1)、(x2, y2)、(x3, y3)分別代表三角形的三個頂點。例如：某三角形之三個頂點分別為(5, 4)、 (6, 1)、(10, 5)，則其Ａ及面積Ｓ分別為：

>> A=[1 5 4;1 6 1;1 10 5]

A =

     1     5     4
     1     6     1
     1    10     5

>> S=det(A)/2

S =

     8

其面積為8個單位。

任意形狀之面積

求一個任意三角形之面積並不稀奇，問題是若要求任意形狀之面積時，其實可以將其分割為成許多大小不同的三角形，用程式計算後，再予以加總。因而再複雜的形狀，也可以因而得解。這就是網絡分析的重點。以下圖為例，這個多邊形由六點組成，若區分為三角形則可改由四個三角形組合而成。設其各點之對應座標及各三角形點之組合如下表：

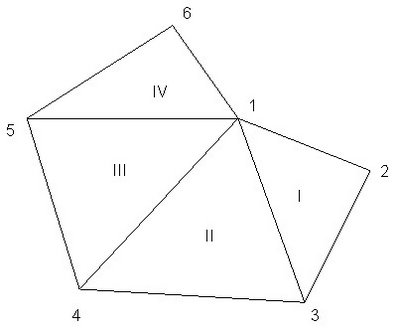
表一、多邊形各點對應值
點號       X       Y    Z(高度)
=====    ====    ====   ======
 1         1       6      3
 2         3       5      5
 3         2       2      6
 4        -2       3      8
 5        -4       6      5
 6         0       8      4

表二、三角形編號對照表

三角形編號      對應點
==========  =i=   =j=   =k=
    1        1     2     3
    2        1     3     4
    3        1     4     5
    4        1     5     6

表一中另列有Z值，此值為對應該平面點之高度或某一特定函數。因此，除計算ＸＹ面之多邊形面積之外，若為三度空間之座標，實際上亦可計算其體積、上層之表面積等。

計算體積時，可以就每一個三角形底面積乘以對應之高（即為Ｚ），為獲得平滑資料，可以取其三頂點對應之高度作平均，亦即每一個三角形對應之體積應為：

Ｖ＝[det(A)/2] (Zi+Zj+Zk)/3

其中之i、j、k分別為每個三角形之對應頂點（即表二之值）。

表面積之求法較為複雜。基本上曲面之表面必須利用積分的形式，分成三角形之網絡亦可求得，此時必須針對三角形之頂部表面考慮，然後進行累加。亦即，設z=u(x,y)為座標點(x,y)之函數，則



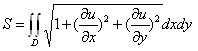
此式中，U為x,y之函數，亦可視為第三座標z值。在三角形之最小單位中，可以利用其三個頂點i, j, k求得其關係式，可聯立如下：

  Ui=u(xi,yi)
  Uj=u(xj,yj)
  Uk=u(xk,yk)

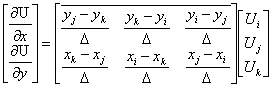
程式內容

% trivolume.m
% Using trianglular method finding irregular areas
x=[1 3 2 -2 -4 0];%nod point
y=[6 5 2 3 6 8];
z=[3 5 6 8 5 4];
elements=[1 2 3;1 3 4;1 4 5;1 5 6];%trangle code
TA=0;TV=0;TS=0;
for i=1:length(elements(:,1)),
   p1=elements(i,1);p2=elements(i,2);p3=elements(i,3);
   A=[1 x(p1) y(p1);1 x(p2) y(p2);1 x(p3) y(p3)];
   delta=abs(det(A))/2;
   TA=TA+delta;%cumulative area
   TV=TV+delta*(z(p1)+z(p2)+z(p3))/3;%cum. volume
   B=[y(p2)-y(p3) y(p3)-y(p1) y(p1)-y(p2);
       x(p3)-x(p2) x(p1)-x(p3) x(p2)-x(p1)];
   ZZ=[z(p1) z(p2) z(p3)]';
   UU=B*ZZ/det(A);
   ES=delta*sqrt(1+UU(1)^2+UU(2)^2);
   TS=TS+ES;
end
disp(['The bottom area:',num2str(TA)]);
disp(['The total volume:',num2str(TV)]);
disp(['The total surface area:',num2str(TS)]);

執行範例：

>> trivolume
The bottom area::23.5
The total volume::118.8333
The total surface area::34.444