10.8 斜角指令之應用

diag對角指令

在前面討論到解一些聯立方程式時，主矩陣之安排及其內容是重要的項目。一般小程式中，其處理之矩陣不大，故應用時不會有什麼問題。以熱流之計算為例，依數值分析法題意中所分之元素A然很大，故其聯立之方程式仍然甚少。解題過程中不會發生容量與計算時間之問題。但在實際的數值分析題目中，其所分的節點很多(如一、二千點)， 則所需處理的方程式增多，矩陣因而變大。不但佔去大部份之記憶體，而且浪費許多電腦計算的時間。而且在這些代表的矩陣中，大部份之項目均為零，不但沒效率，而且輸入均是困擾。為此，matlab有幾個特別處理對角項輸出入之指令，如：

A = eye(5)
A = diag(X)
A = diag(X,k)
Out=blkdiag(a,b,c)

指令eye主要在造出一個對角項為1之方形矩陣，前面也有許多實例之應用，如：

A=eye(5)
A =

  1     0     0     0     0
  0     1     0     0     0
  0     0     1     0     0
  0     0     0     1     0
  0     0     0     0     1

故若欲得到對角線上之相同元素項，可以直接用eye()乘以某一常數項即可。然而有些矩陣並不是方形，而且其所需填入之值也並不一定在對角線，此時若一一輸入又不勝其煩。此時必須借助diag這個指令。在使用這個指令之前，對於對角線方向之元素，必須有統一的說法，其指令才能得心應手。首先，可參考下圖方型矩陣的元素相關位置：



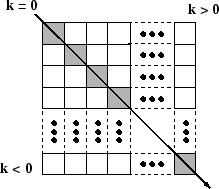
在矩陣中，凡是成45度角之元素均可稱為對角元素。為標明不同之位置，可以用一索引 k 表示。即在對角線正中間者可以設 k=0，在平行而且在此對角線之右上者，則依序以k=1, 2, 3,...表示，以下（左下角）者以k=-1, -2, -3,...表示。所以右上方k值為正；左下方k值為負。利用diag指令，Ｘ參數為一向量，即為欲填入對角線之值，可為行向或列向。k值之預設值為零，故不設定k值表示為對角線上之項目。例如：

>> A=diag([1 2 3 4])

A =

  1     0     0     0
  0     2     0     0
  0     0     3     0
  0     0     0     4

>> A1=diag([1 2 3 4],1)

A1 =

  0     1     0     0     0
  0     0     2     0     0
  0     0     0     3     0
  0     0     0     0     4
  0     0     0     0     0
>> A2=diag([1 2 3 4],-3)

A2 =

  0     0     0     0     0     0     0
  0     0     0     0     0     0     0
  0     0     0     0     0     0     0
  1     0     0     0     0     0     0
  0     2     0     0     0     0     0
  0     0     3     0     0     0     0
  0     0     0     4     0     0     0

上式，對角線元素之鉗入位置可見是依 k 值而定。不過有一點必須注意的是：一旦 k 的絕對值不同於零，所形成之方矩陣會變大，其大小正好比原來Ｘ項之長度加上k值之絕對值。所以對角線元素之位置愈偏離，其所得之矩陣會愈變大。故若要維持原來的大小(4 X 4)，則必須稍作改變，例如，A2可以調整如下：

>> A3=A2(3:end,1:end-2)

A3=

  0     0     0     0     0
  1     0     0     0     0
  0     2     0     0     0
  0     0     3     0     0
  0     0     0     4     0

若欲產生綜合兩對角之項目則可執行指令如下：

>> eye(5)+A3

ans =

  1     0     0     0     0
  1     1     0     0     0
  0     2     1     0     0
  0     0     3     1     0
  0     0     0     4     1

除此diag指令之外，MATLAB又有一個組合指令blkdiag，可以將任何大小之矩陣依矩陣之對角方向集合成一個大矩陣，例如：

>> C=[1 2 3;4 5 6]

C =

  1     2     3
  4     5     6

>> M=eye(3)

M =

  1     0     0
  0     1     0
  0     0     1

>> out=blkdiag(C,M,C)

out =

  1     2     3     0     0     0     0     0     0
  4     5     6     0     0     0     0     0     0
  0     0     0     1     0     0     0     0     0
  0     0     0     0     1     0     0     0     0
  0     0     0     0     0     1     0     0     0
  0     0     0     0     0     0     1     2     3
  0     0     0     0     0     0     4     5     6