10.3 範例六、det & rank 指令之應用

det & rank 指令

利用左除法的求解過程甚為簡單，但有時並不一定有解，有時也可能有多組解。聯立方程式中，型式上其變數與方程式之數目相同，應可以得解。但有些方程式是相依的，或者其中方程可能由其他兩式相互加減而得的結果，此時即無法無法獲得唯一解，因此過程上仍需先行檢驗。行列式值與聯立方程式求解有密切的關係。其值若為零，所得之解可能為非唯一組解；若不為零，則可能得到一組解。在MATLAB中，可以使用位階指令rank檢驗。

舉例：

一魔術函數造成之矩陣Ａ，其行列值及位階分別由det & rank 指令進行檢驗：

　　A=magic(4);
　　det(A)
　　rank(A)

ans =     0
ans =     3

矩陣Ａ雖為4x4，利用行列值檢視，其值為det(A)=0，表示無法獲得單一解。同樣利用rank位階指令檢查，其結果為3階，兩者均顯示與矩陣Ａ相關之聯立方程式可能為多組解。

要檢測一組聯立方程式是否有解，使用上述rank的指令功能可以研判。例如檢測AX=C這一組聯聯立方程式，先求rank(A)與 rand([A C])之階值，後者[A C]稱為增廣矩陣(Augrmented matrix)。若所得兩個階值相同，且其階值等於變數個數時，應為有解且其解屬唯一。若階值小於變數個數時，其解應為多數解，其變數可用兩者之差數之線性組合表示。

範例：

　A=[6 -3 5;10 4 -8;-6 2 3];C=[12 -20 15]';
　R1=rank(A)
　R2=rank([A C])

　R1 =     3
　R2 =     3

由於兩者之階值相同，表示其解存在且為唯一。下面就一個多數解的例子進一步說明：

　A=[3 2 1; 10 -25 5];C=[5000 2000]';
　R1=rank(A),R2=rank([A C])
　R1 =     2
　R2 =     2

顯然這組方程式應有解，但由於階數2小於變數個數3，故其解為多數解。利用左除法亦可得到其中一解，即令T3等於零時，所得之答案。其過程如下：

　T=A\C
　T =
     1357.9
     463.16
          0

範例六：

有一電路如圖，接於一電源Ｖ上。試求通過各電阻器上之電流。



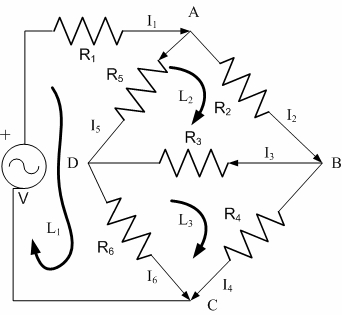
根據克希荷夫Kirchhoff定律，可以選定三個迴圈建立屬於電壓降之三項聯立方程式，及電流經由Ａ、Ｂ、Ｃ三點產生分流時所能建立之四個關係方程式得之：



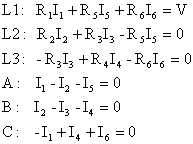
整理此組聯立方程式，其電流變數Ｉ有五項，其方程式有五組，故應可得解。茲以矩陣[R][I]=[V]表示，利用左除法即為[I]=[R]\[V]。其各變數矩陣分別為：



　 　

程式內容

function Curr=ele_amp(v,r)
% Prog using Kirchihoff's law to find the currents in a circuit.
% Inputs:
%   v: Voltage of generators. volts
%   r: the resistances  r=[r1 r2 r3 r4 r5 r6], in Kohms.
% Outputs:
%   Curr: currents through resistors [c1 c2 c3 c4 c5 c6], in mA
% Example: current=ele_amp(100,[1 1 2 5 5 10])
V=[v 0 0 0 0 0]';
R=[r(1)   0     0    0  r(5)  r(6);
    0  r(2)  r(3)    0 -r(5)     0;
    0     0 -r(3) r(4)     0 -r(6);
    1     0    -1    0    -1     0;
    0     1    -1   -1     0     0;
   -1     0     0    1     0    -1];
Current=R\V;Curr=Current';

執行結果：

>> current=ele_amp(100,[1 1 2 5 5 10])
current =       8.0338        17.97       3.1712       14.799       4.8626       6.7653
>> current=ele_amp(100,[0 1 2 5 5 10])
current =
     8.7356        19.54       3.4483       16.092       5.2874       7.3563